人工智能原理

引言

McCullochPitts 一元一次方程

海底生物小蓝的只能基于一元一次方程，

假设它需要完成一个任务，吃到豆豆

image-20220707142013298

但豆豆是有毒的，并且毒性于大小有关，如果吃到具有毒性的豆豆小蓝就失败了。

image-20220707142130792

要做到这一点就需要使用函数来进行认知。

比如$E=MC^2$ 自然界有很多事务，如果你愿意也可以使用函数去描述它，虽然不一定很严格但是很多情况下是有效的。比如小狗的可爱程度和眼睛的大小关系

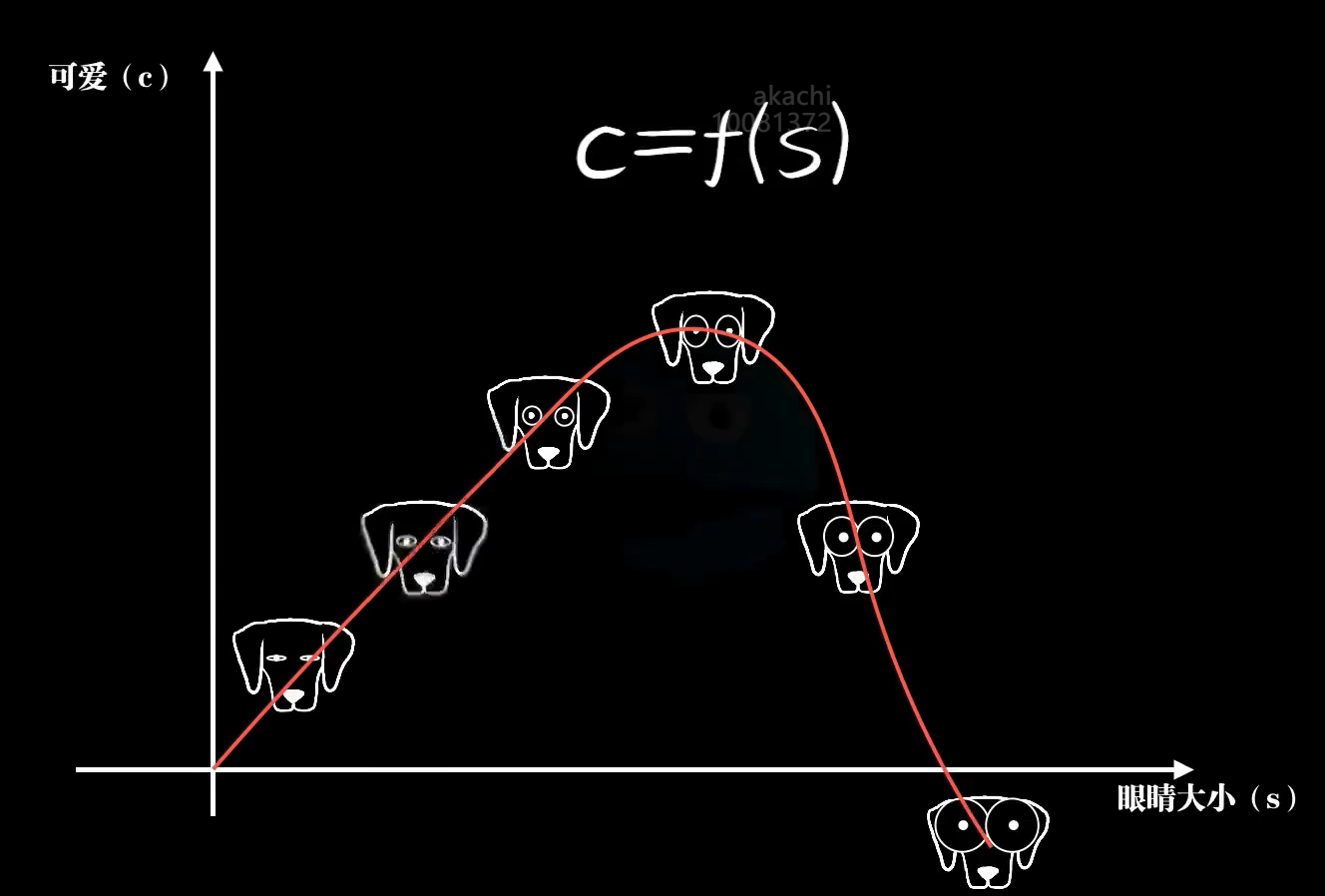
​ image-20220707142510850

回到上面的问题中

image-20220707142547600

豆豆的毒性是一个一元一次方程，W是斜率，X是豆豆的大小也就是自变量，Y则是毒性也就是我们需要知道的标签。

实际是使用函数去描述神经元模型早在１９１４年就被提出了mcCulloch-Pitts模型

image-20220707142751694

image-20220707142922616

图中是个神经元，左侧的连接是树突，在函数中代表子变脸而右侧的则是轴突。神经元由树突输入信号并由轴突输出信号，如果树突只有一个那么这个神经元就对应一个一元函数。而参数W则是属于树突的参数，我们在这里称之为权值。

image-20220707143223974

全职决定了这个树突对轴突输出信号时的权重。

在mcCulloch-Pitts模型中还有一个偏置项ｂ，用于决定激活函数，是否运行函数的输出。

image-20220707143922947

回到小兰的话题中来，选择这个关于大小的一元函数中的权重ｗ是它活下去的关键，这个ｗ如果过大或过小都是偏离现实的直觉，只有恰到好处且符合事实的直觉才能帮助它活下去。

Rosenblatt感知器模型

由于以上McCullochPitts模型中并没有考虑如何便跟权重，也就不涉及到机器学习于训练。所以如果新提出来的感知器模型中对它进行了修正。

image-20220707144936090

在感知器模型中W权重会根据实际拿到的值进行便跟，比如在以上我们的小蓝吃了个豆子，函数告诉他这颗豆子毒性很低只有0.1结果吃了发现毒性时0.5，显然在我们的函数中毒性与大小的函数斜率太平了，我们需要调整它。于是我们用实际毒性-测量毒性=0.4 使用它来直接调整斜率 w+0.4=0.5

另外为了保证正负值都能够被包含这个公式应该是$w+α+VX=w’$ 所以感知器模型的公式如此

  • w 斜率
  • α 学习率
  • v 误差斜率(实际斜率-当前斜率)
  • x 自变量
  • w’ 修改后的斜率

这个α在修在

罗森布拉特(本算法的提出者)第一次从数学上提供了w最终完成收敛的数学证明